¡Vamos a poner manos a la obra!
Conociendo la forma gráfica:
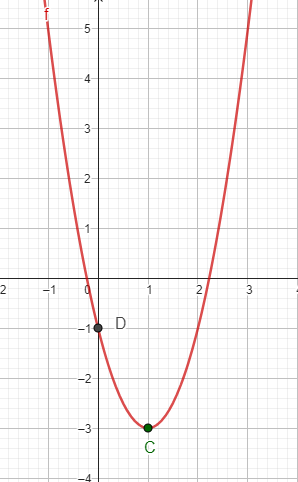
Conociendo que una de las formas analíticas se escribe:
y = a(x-h)2 + k
Además, puedo visualizar en el gráfico que:
- Del punto D= (0,-1) puedo extraer el valor de x=0 y el de y=-1.
- El punto C= (1, -3), es el vértice de la parábola. Entonces h=1 y k=-3
- A a no la conozco.
Para lograr el cálculo de a sustituyo en la ecuación lo que conozco y la hallo.
La ecuación me queda: -1= a (0-1)2+(-3).
Ahora realizo cuentas obteniendo que -1= a (-1)2+(-3)
Continuo operando dando: -1=a1+(-3).
Reordenando: -1=a-3 y despejo a: 3-1=a.
Entonces a=2.
Esto me lleva que teniendo muy presente que D es solo un representante de los puntos que forman la parábola.
La representación de forma analítica de la parábola que está en la gráfica es:
y = 2(x-1)2 - 3
De donde trabajando el cuadrado del binomio, distributiva y reduciendo llego a la expresión y = 2x2-4 x -1, que es una de las formas de expresar a la parábola más tradicional y ya analizada anteriormente.