Si llamamos r2 al radio del segundo envase, tendremos que h = 2r2, luego, su volumen estará dado por: 
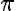· r22 . 2r2 = 1000.
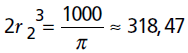
r23 ≈ 159,24, luego r2 ≈ 
De forma similar a las raíces cuadradas, se puede justificar si a y b son números reales y a < b, se cumple que 
.
Usemos este hecho para aproximar . Observa:
(5,5)3 = 166,375 y (5,4)3 = 157,464
Podemos notar que r2 se encuentra entre 5,4 y 5,5; sin embargo, r2 es más cercano a 5,4 que a 5,5. Probemos con 5,42.
(5,42)3 = 159,220088. Esta estimación es más cercana aun. Entonces, la longitud del radio del cilindro es aproximadamente 5,42 cm, mientras que la altura será aproximadamente 10,84 cm.
La aproximación encontrada nos permite comparar raíces cuadradas con raíces cúbicas, en este caso 
> , ya que 5,64 > 5,42.
Por lo tanto, el segundo envase tiene menor radio.