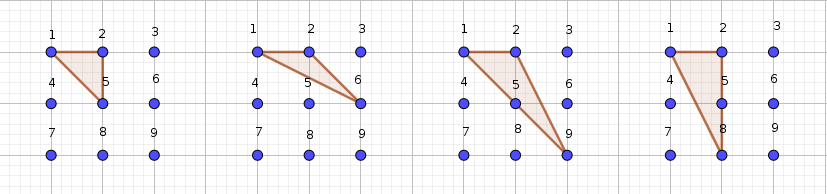
Estrategia 2: nos enfocamos en los vértices

Otra estrategia de conteo que podemos utilizar es numerar los puntos del geoplano y luego ir eligiendo los vértices de cada triángulo.

cuadricula de 3x3 con puntos numerados

Con puntos 1 y 2 de vértice

Si elegimos como vértices los puntos 1 y 2 analizaremos cuántos triángulos distintos obtenemos al considerar el tercer vértice entre los restantes.

Observamos que son los 4 de la figura.

Porque si elegimos los puntos 1, 2, 3 no hay triángulo, y si elegimos 1, 2 , 4 o 1, 2, 7, quedan triángulos iguales a los que ya tenemos contados.

Observa que si elijo las parejas de puntos 1 y 4, 3 y 2, 3 y 6, 9 y 6, 9 y 8, 7 y 4, 7 y 9, estaría contando triángulos de igual forma y tamaño, pero en posiciones distintas.

vertices 1 y 2

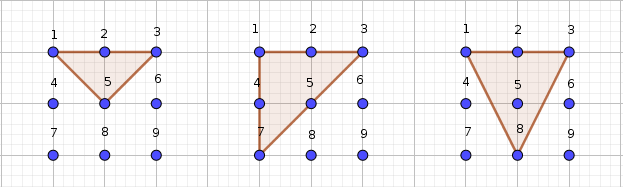
Con puntos 1 y 3 de vértice

Vemos que hay 3 triángulos más:

Si eligiéramos (1, 3, 9) o (1, 3, 4) o (1, 3, 6) quedarían formados triángulos de igual forma y tamaño que los de la figura, pero en distinta posición.

El mismo razonamiento se puede hacer si, en vez de partir del vértice 1 y 3, lo hacemos de los pares de puntos 3 y 9, 9 y 7 o 1 y 7.

Seguimos con el vértice 1

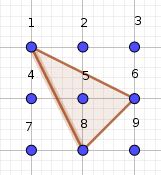
Partiendo del vértice 1, el único caso que no hemos considerado hasta ahora es el triángulo de vértices: (1, 8, 6)

Con los puntos (3, 4, 8); (9, 2, 4) y (7, 2, 6) se obtienen triángulos de igual forma y tamaño que éste en diferentes posiciones.

De esta manera ya contamos todos los triángulos que tienen por lo menos un vértice en un esquina del geoplano y hemos encontrado 8 diferentes.

Vértices en puntos medios

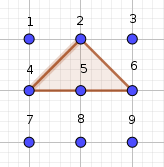
Veamos ahora si elegimos como vértices, no las esquinas del geoplano, sino los puntos medios entre dos esquinas ( 2, 6, 8, 4).

Usando tres de esos puntos obtenemos siempre triángulos de igual forma y tamaño, en distinta posición, y este tipo de triángulo ya lo habíamos contado en los casos anteriores.

Vértice en centro

Nos falta pensar ahora si elegimos el punto central del geoplano. Pero ese punto se tiene que elegir además con dos de los puntos que están en el contorno, por lo que en los casos anteriores ya contamos los triángulos que tienen a ese punto como uno de sus vértices.

Conclusión

Existen solo 8 triángulos de diferente forma y tamaño en una geoplano de 3x3.