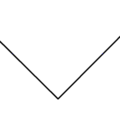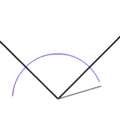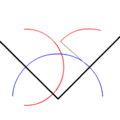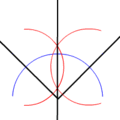
Recuerda que la bisectriz de un ángulo es la semirrecta interior que divide el ángulo en dos iguales. Todos los puntos de la bisectriz equidistan de los lados del ángulo.

En el siguiente video veremos las bisectrices de los ángulos interiores de un triángulo y sus principales propiedades utilizando GeoGebra:

Abre GeoGebra y sigue los pasos indicados:

1.- Dibuja un triángulo ABC

2.- Construye las bisectrices de dos de los ángulos interiores del triángulo.

3.- Halla el punto de intersección. Comprueba que la tercera bisectriz pasa por el mismo punto.

4.- Mueve los vértices del triángulo y observa lo que ocurre.

5.- Las tres bisectrices de un triángulo hacen intersección en un punto que se llama incentro. ¿El incentro es siempre un punto interior?

6.- Nombra In al incentro.

7.- Oculta las bisectrices y deja sólo el punto In.

8.- Mide la distancia del punto In a los lados del triángulo. (Recuerda que para medir distancias necesitas perpendiculares).

9.- Mueve los vértices del triángulo y observa lo que ocurre.

10.- ¿Por qué razón el punto In está a la misma distancia de los lados?

11.- Construye la circunferencia inscrita en el triángulo.